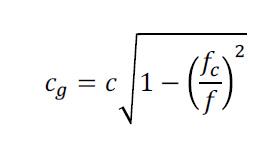During a research trip to Antarctica, Dr. Peter Neff, a postdoctoral associate in the University of Rochester’s Ice Core Lab, recorded the sound ice made when dropped 90 meters into a glacier borehole. He and his colleagues began to do it over and over and speculated as to what caused the crazy sounds.
The recording got about 8 million hits across various platforms, with many people wondering about what caused the odd sounds made by the plummeting ice.
Enter Mark Bocko, professor and chair of the electrical and computer engineering department at Rochester, and colleagues. They took a look and did some research and found that the answer is sound dispersion in acoustic waveguides. Well, you probably knew that part. It's a little more involved. First, have a listen.
They write: "As the piece of ice falls down the hole, it scrapes and bounces off the edge of the borehole. You can hear the frequency of this sound decrease as the ice chunk picks up speed the further down the hole it gets. The decrease in frequency is the Doppler effect, the same effect that causes a car horn to drop in pitch as it drives past you.
"After the ice chunk hits the bottom of the borehole, you can hear a “ricochet” noise, which is caused by the slightly different ways the sound from the impact propagates back up the borehole. The acoustic wave for the “heartbeat” impulses travels straight up the borehole, while the other sound waves bounce back and forth off the side-walls of the borehole on their way up. This causes different frequencies to travel at different speeds. The high frequencies travel fastest and get to the top first while the low frequencies lag behind and arrive later.
"The spacing of the “heartbeat” noises after the ice impacts is determined by the depth of the hole and the speed of sound in air. In this case, the speed of sound in air at -20 degrees Celsius is 318.9 meters/second; it takes sound about half a second to make one round in the 80-meter-deep borehole."
The speed of propagation of acoustic energy as a function of frequency (the so-called group velocity) for each mode can be represented by a function of the form:

where fc is the cutoff frequency and f is the frequency of the acoustic wave. Note that the group velocity goes to zero below the cutoff frequency, i.e., acoustic energy cannot be propagated by a mode below its cutoff frequency. Far above the cutoff frequency acoustic energy is transported by the mode at the speed of sound in open air, and as the cutoff frequency is approach from above the propagation speed decreases, going to zero at the cutoff frequency,
Read their full analysis here.
References:
Morse, Philip McCord, and K. Uno Ingard. Theoretical acoustics. Princeton university press,
1968, pp 509 – 514.
Skudrzyk, E. “The Foundations of Acoustics: Basic Mathematics and Basic Acoustics. Wien.”
(1971), pp 430-435.