Turbulent flows are common, from large-scale atmospheric and ocean currents to microscopic bacteria suspensions. These swirling structures have also inspired artists, notably van Gogh’s The Starry Night. Lewis Fry Richardson, a British physicist and meteorologist, was an early explorer of turbulent flows as they are necessary for weather prediction. He wrote,
“Big whirls have little whirls that feed on their velocity,
and little whirls have lesser whirls and so on to viscosity.”
Those swirls are a dramatic feature of Starry Night and are the subject of a new study looking at the painting from a physicist’s point of view. While Starry Night is an unchanging snapshot in time, the researchers used the luminance, the intensity of light emitted from the swirls, to characterize “the kinetic energy information from these patterns.”
What is turbulence?
That is an excellent question, but it remains unsolved. [1] Werner Heisenberg, when asked what he might ask God, replied:
"When I meet God, I am going to ask him two questions: Why relativity? And why turbulence? I really believe he will have an answer for the first."
Fluids, whether gases or liquids, flow. They have quantifiable properties like velocity and viscosity and are governed by the “laws” of physics we learned in school, specifically the conservation of mass, energy, and momentum. Of more specific interest in understanding how flow becomes turbulent, we need to momentarily consider viscosity – which is a measure of friction between the layers of molecules in a flowing liquid. As the friction between the layers increases, an increase in viscosity, the layers of flow pull against one other and hamper that flow, e.g., honey vs. maple syrup. As the difference in flow rate between the layers increases, a condition described as shear, particles at the interface of the layers will begin to rotate.
Mathematicians have developed a formula to describe turbulence, the Navier-Stokes Equation.
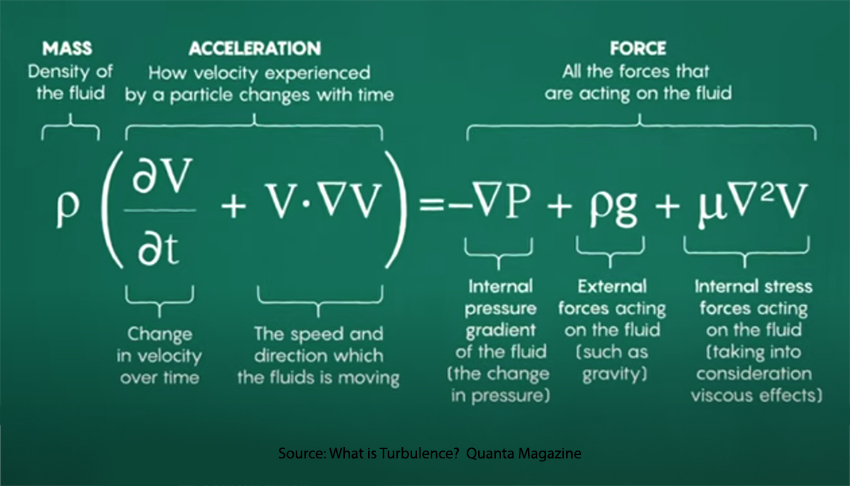
Undaunted by the symbology, the sharp observer will note that the particular fluid identified is nowhere in the equation. Turbulence is a feature of fluid flow, not of the fluid.
Four key features characterize turbulence:
- Irregularity: turbulence is highly irregular and chaotic and can only be described statistically.
- Diffusivity: The energy in turbulent flow accelerates the mixing (diffusion) of a fluid’s components (momentum, heat, and mass transfer), making it more homogenous.
- Rotationality: Because of those frictional forces resulting in shear, turbulent flow is always rotational, generating those three-dimensional swirling patterns you see in smoke or Starry Night. These “vortices” stretch as the flow continues, creating increased rotation because of the conservation of angular momentum while simultaneously thinning in the perpendicular direction. Vortex stretching plays a crucial role in turbulence’s energy cascade, breaking larger vortices into smaller ones.
- Dissipation: At some point within those smaller vortices, viscosity forces overtake all those rotational forces, and the turbulence ends. Turbulent flows die out quickly when no energy is supplied.
The onset of turbulence can be predicted using the Reynolds number, which measures the ratio of inertial forces (causing fluid movement) to viscous forces (resisting movement). The Reynolds number quantifies the relative importance of these two types of forces for given flow conditions. It is a guide to when turbulent flow will occur in a particular situation. Turbulent flows always occur at high Reynolds numbers. When the Reynolds number is high enough, turbulence is the same for liquids and gases, becoming independent of the properties of the fluid.
But we have digressed.
“Vincent van Gogh, as one of the most notable post-impressionist painters, had a very careful observation of turbulent flows: he was able to reproduce not only the size of whirls/eddies, but also their relative distance and intensity in his painting.”
“The Starry Night” [2] portrays the view from van Gogh’s asylum room in Saint-Rémy-de-Provence, France, just before sunrise, with an added imaginary village and swirling sky. The painting is considered van Gogh's masterpiece and one of Western art's most recognized works. In the painting, 14 visible swirling structures, or "eddies," can be identified, with diameters ranging from 4.2 cm to 27.6 cm. In an even deeper dive, the physicists considered the paints themselves, and because they were a mix of a high-viscosity liquid, linseed oil, with a stone powder as the colorant, the paint within the whirls demonstrated turbulence in their mixing.
Art and science are often in dialogue, similar to culture and science. While van Gogh was not a physicist, he could closely observe, just as a scientist must, although he expressed his observations with paint rather than numbers. The researchers were not the first to be drawn to the painting; earlier work suggested that the painted patterns closely mimicked the molecular clouds forming galactic nurseries.
There you have it, “The Starry Night” is not just a pretty picture; it's a masterclass in turbulence. Whether he knew it or not, Van Gogh painted a fluid mechanic’s dream, complete with swirling vortices and energy cascades. And while physicists may marvel at the mathematical elegance of those whirls, the rest of us can just enjoy the fact that sometimes, chaos is beautiful—whether it's in a painting or a weather forecast.
[1] The Clay Mathematics Institute has offered a millennium prize of $1 million for proving whether the Navier-Stokes equations always work or sometimes fail, along with six other well-known complex mathematical problems.
[2] By Vincent van Gogh from Google Arts & Culture, in the Public Domain, on Wikipedia
Source: Hidden Turbulence in van Gogh’s The Starry Night
What is Turbulence Quanta Magazine
Chuck Dinerstein, MD, MBA
Director of Medicine
Dr. Charles Dinerstein, M.D., MBA, FACS is Director of Medicine at the American Council on Science and Health. He has over 25 years of experience as a vascular surgeon.
